过去二三十年,以量子比特(quantum bit, qubit)为量子信息基本单元的量子技术取得了一系列里程碑式的科学进展,例如无漏洞贝尔非局域实验证明、卫星中继量子通信、量子计算优势实验证明、小时级超长时量子存储等。在物理底层,量子比特通常由高度人工可操控的二能级体系来实现,例如光子、超导、离子和固态体系等量子体系。然而,自然界广泛存在的量子体系实际上天然地含有多个量子化本征模式,包括原子中电子能级结构、分子振动模式等,从而蕴含了非常丰富的物理化学特性。有意思的是,上述人工可操控的量子体系,通常也含有多个本征模式,只是因为高维量子操控技术还不成熟,使得人们在过去更多地关注于二进制量子比特信息科学与技术的发展。
近年来,高维量子信息科学与技术通过人工操控高维量子位(quantum dit, qudit)来实现量子信息的编码、处理、传输和存储,有望实现更加强大的量子计算、量子通信和量子模拟等功能,因此引起了量子信息领域科学家们的极大兴趣。例如,高维量子位和高维量子纠缠态已经在光子、超导、离子和固态等体系中实现,并被应用于广义贝尔不等式的强违背实验证明,高维量子纠缠被认为可以降低贝尔非局域的无漏洞证明条件;对高维量子位的量子调控能力也显著提升,已实现了多种高维单、双量子位逻辑门操作;高维量子技术也在抗噪声量子密码分发、高速率随机数发生、高维量子隐形传态、高维量子态存储和复杂分子系统模拟等方面,发挥了重要作用;另外,基于线路模型和测量模型的高维通用量子计算都已被理论证明是可行的,且有助于提升量子计算算法的性能、降低量子纠错所需物理资源等。更宽泛地讲,寻找一种与自然更亲和的人工高维量子体系,并对其进行操控以达到更强、更快、更精确的量子信息处理能力,对基础研究和前沿探索均具有重要意义。然而,对于高维量子计算的实验研究还非常稀缺,比较相关的工作是最近加拿大国立科学研究院、美国普渡大学在光学体系报道了高维簇态的制备和简单计算演示,这主要是因为高维量子计算对单、多量子位的操控能力、操控精度、操控任意性、可编程性以及计算结果可读取性等,提出了更高更苛刻的要求,而目前绝大部分高维量子技术还无法满足上述实验条件。
基于互补金属氧化物半导体制造工艺的硅基集成光量子芯片技术为高维量子计算和量子信息处理提供了可能。硅基光量子芯片具有可制备复杂量子纠缠态、量子操控保真度高、可编程重构和可大规模集成量子器件等优势。yl8cc永利官网现代光学研究所、人工微结构和介观物理国家重点实验室、纳光电子前沿科学中心、“极端光学创新研究团队”王剑威研究员和龚旗煌院士研究团队,在前期工作中发展了一种硅基光量子芯片上多路径编码的高维量子信息技术,例如实现了高维体系量子相干性和广义波粒二象性的实验测量(Nature Communications 12, 2712 (2021))、十五维度量子纠缠态的精确制备和可编程操控及其量子非局域等基本物理特性的测量(Science 360, 285 (2018)),进而利用高维量子比特等价量子比特的方法演示了八比特簇态光量子计算功能(Nature Physics 17, 1137 (2021))。然而,为了实现高维量子位直接编码的高维量子计算功能,还需要实现高维单量子位逻辑门、高维双量子位纠缠逻辑门、及其高维组合逻辑门,并要求其具有高编程可操控性、高保真度和可测量读取的能力,这些关键技术的缺失一直限制了高维量子计算的发展。
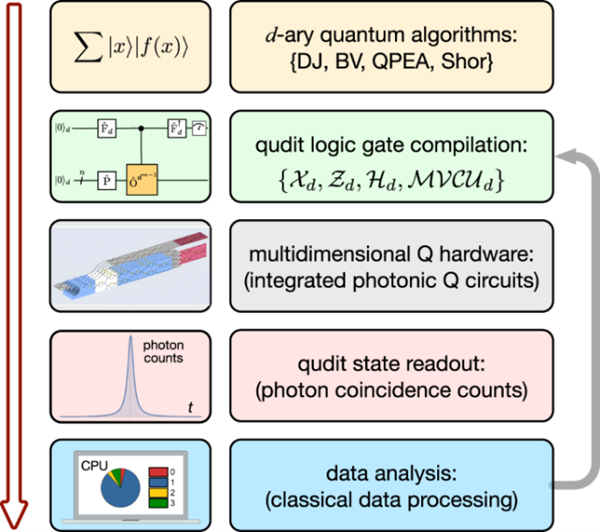
图1 至上而下的高维量子计算架构(从顶层需求到物理底层实现、从量子算法到量子门操作)
近日,王剑威研究员和龚旗煌院士课题组与合作者实现了一款基于大规模硅基集成光量子芯片的可编程高维量子处理器。该处理器单片集成了约450个光学元器件和116个可编程器件,在单个芯片上实现了高维单量子位和双量子位的初始化、操作和测量。全功能集成和强可编程性提供了一种至上而下、从算法到量子门操作、从顶层需求到底层物理实现的高维量子计算架构(图1),用户只需要对处理器输入相应的量子算法需求,通过编译成高维单双逻辑门的组合,进而编程重构物理底层的光量子芯片线路结构,来实现算法运行和计算结果输出。也就是说,不同的计算任务可在软件层面编译成不同的量子线路,然后在硬件层面通过编程重构光量子芯片的物理配置来执行该量子线路,从而在同一处理器上可执行多种量子计算任务。联合研究团队编程重构该处理器超过百万次以上,实现了一系列高保真量子逻辑门操作,执行了多种重要的高维量子傅立叶变换类算法,包括高维Deutsch-Jozsa和Bernstein-Vazirani算法、高维量子相位估算和高维Shor大数分解(求阶)算法;并通过高维量子算法的有效运行,首次成功实现了高维量子计算的原理验证演示,可提升量子计算容量、计算精度和计算速度等,将有助于研制大规模光量子计算和量子信息处理芯片。
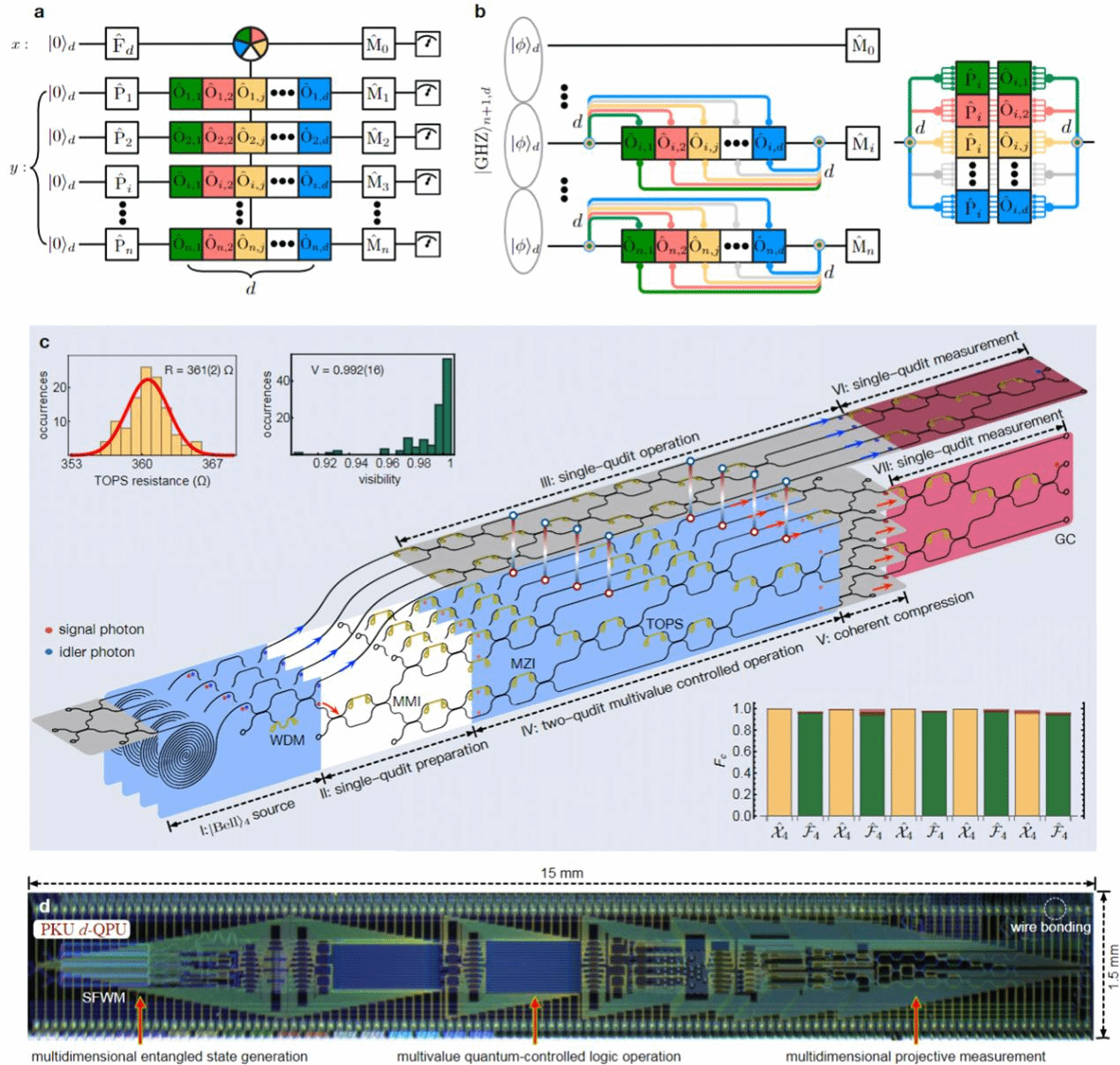
图2 高维量子处理器的量子线路图(a),实现方案图(b),光量子芯片结构图(c),显微镜照片(d)
联合研究团队提出并实现了一种可扩展的高维光量子计算方案,其核心是实现多个高维量子位的多值受控纠缠逻辑门(图2(a-b)):通过多光子高维纠缠态引入高维量子位间的受控纠缠操作,对受控量子寄存器的每个高维量子位进行希尔伯特空间扩展并进行局域操作,最终将态空间进行相干压缩处理。图2(c-d)为双高维量子位的高维量子处理器芯片的线路图和显微镜照片,单片集成了约 450 个光学器件,包括 4个自发参量四波混频量子光源和116个可编程重构热光移相器等,该量子处理器芯片可以通过电子器件驱动实现灵活远程控制和自由配置。该光量子芯片可实现任意的单量子位四维量子门(例如X4、Y4、Z4、H4、F4等,分别为四维广义的泡利门、Hadamard门和傅立叶变换门),双量子位多值受控任意四维幺正门(例如C4X4、C4Z4和C4H4分别为四维广义的受控非门、受控相位门和受控Hadamard门)。通过量子态层析和量子过程层析等测量手段,实验得到了高维单量子位操作的保真度约为98.8%,高维双量子位操作(如C4X4门)的保真度可达95.2%,片上产生并测量到完整四维贝尔态的平均保真度约为96.7%。
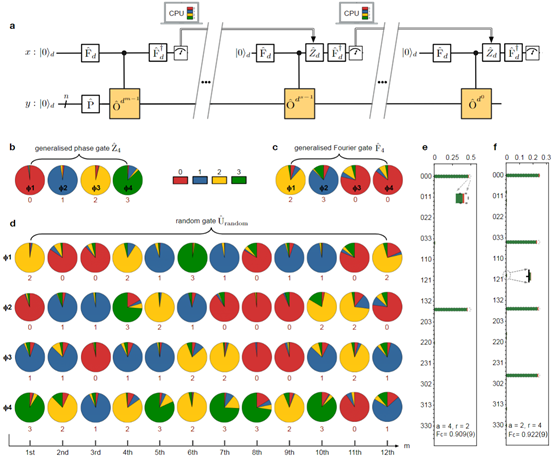
图3 高维量子相位估计算法和量子快速大数分解(求阶)算法的实验结果。(a) Kitaev迭代量子相位估算算法和迭代求阶算法的高维量子线路图;(b-d) 广义相位门、傅里叶门和随机门的量子相位估计计算结果,红色数字下标为理论结果;(e-f) 高维量子求阶算法的输出概率分布实验结果,分别对应a=4和a=2的情况。
量子傅立叶变换类算法是量子计算最核心的基础算法之一,联合研究团队在高维量子处理器上演示了多种推广的高维量子傅立叶变换算法,其核心是利用高维多值受控逻辑门进行函数的量子并行计算,同时利用高维傅立叶变换实现多路径量子干涉来获取计算结果,而这种高维量子并行性会比二维体系更强。联合研究团队首先验证了推广的高维Deutsch-Jozsa算法和Bernstein-Vazirani算法,前者可一次确定多值函数f(x)是常数还是平衡函数,后者可一次测量确认仿射函数的近似表达式;利用高维编码可实现更长数据串的多值函数判断、更复杂仿射函数的计算。进一步,在高维量子处理器上运行了高维量子相位估计和量子求阶算法,这两种算法是量子化学模拟和大数分解等前沿应用的核心。研究工作采用了Kitaev迭代方法来高效执行高维量子相位估计和量子求阶算法,其量子线路如图3(a)所示,其计算容量由y寄存器的高维(d维)量子位数目(n)决定,而计算精度由x寄存器的m步迭代次数决定。实验结果表明,高维量子处理器可快速且精确计算酉矩阵的本征值,包括高维相位门、高维傅立叶门和高维随机酉门,如图3(b-d)所示(每个饼图表示一步迭代计算结果,彩色扇区的面积分别表示四个不同计算基的输出结果)。图3(d)为迭代相位估算得到的随机酉矩的四组本征相位,其计算精度为四进制下的12步精度,而在二进制量子处理器上则需要24步计算以得到相同的计算精度。对于量子求阶算法,其任务是在给定随机选择的a情况下,求数N的阶r,这等价于一个对特征相位为s/r(s小于r)的酉矩阵的相位估计问题,因此可以直接采用d进制相位估计算法来确定r在d中的阶。研究团队在芯片上运行了高维求阶算法,并验证了15=3×5的素数分解问题。以r=2和r=4为例,图3(e,f)分别为三次迭代计算得到的实验结果,每一步迭代输出四元计算结果从而得到s/r本征相的4^3计算精度,其计算保真度分别为90.9%和92.2%。以上实验结果表明,相比于传统二进制量子比特量子计算机,高维量子计算机可以log2(d)倍的计算精度计算函数的阶或酉矩的特征相位,或者说,在计算精度相同的情况下,高维量子计算机的计算速度要快log2(d)倍。
2022年3月4日,相关成果以“可编程高维量子处理器”(A programmable qudit-based quantum processor)为题,在线发表于《自然·通讯》(Nature Communications)。yl8cc永利官网2019级博士研究生池昱霖、2019级硕士研究生黄洁珊、2018级本科生张湛川为共同第一作者;王剑威为通讯作者;主要合作者还包括浙江大学张明助理研究员和戴道锌教授,中国科学院微电子研究所杨妍研究员、唐波高级工程师和李志华研究员,丹麦科技大学丁运鸿高级研究员和Leif Oxenløwe教授,英国布里斯托尔大学Mark Thompson教授,澳大利亚西澳大学Jeremy O’Brien教授,永利集团李焱教授,以及yl8cc永利官网博士研究生茆峻(2020级)、陈晓炯(2018级)、翟翀昊(2021级)、包觉明(2018级)和戴天祥(2019级),2021届本科毕业生周子楠(现日本东京大学博士生)、博士后袁慧宏(现为北京量子信息科学研究院助理研究员)。
上述研究工作得到了国家自然科学基金、国家重点研发计划、北京市自然科学基金、广东省重点领域研发计划,以及永利集团长三角光电科学研究院、北京量子信息科学研究院等支持。
论文原文链接:https://www.nature.com/articles/s41467-022-28767-x


