发布日期:2022-11-27 浏览次数:
供稿:理论物理研究所 |
编校:胡克倩 |
编辑:曲音璇 |
审核:朱世琳
费曼积分是微扰量子场论的基本组成单元,无论是为了基于微扰量子场论进行理论预言,还是为了深刻理解量子场理论,费曼积分都是核心的输入信息。yl8cc永利官网理论物理研究所马滟青课题组经过多年研究,把费曼积分计算问题彻底转换为了线性代数问题,在国际上首次实现了一般性费曼积分的系统性计算。最新成果以“仅用线性代数输入来确定费曼积分”(Determining Feynman Integrals with Only Input from Linear Algebra)为题于2022年11月23日发表在《物理评论快报》(Physical Review Letters)。
随着对撞机实验的快速进展,粒子物理中多个物理过程(比如希格斯粒子在强子对撞机中的产生)的实验精度已经超过理论精度,在不久的将来更多物理过程的实验精度有望大幅度超越目前的理论精度。为了充分利用实验数据,从而能有效地检验粒子物理标准模型及探测超出标准模型的新物理信号,非常迫切需要提高理论预言精度,而多圈费曼积分的计算在多数问题中是主要瓶颈。单圈费曼积分的计算问题早在上世纪70年代末就由两位诺贝尔奖得主 ‘t Hooft和Veltman解决。但是40余年后,人们依然不会计算一般性的多圈费曼积分(即便是稍微复杂的两圈费曼积分)。因此,多圈费曼积分计算一方面极其重要,但同时又是国际公认的难题。
马滟青课题组在过去几年对费曼积分进行了系统深入的研究,提出了“辅助质量流”方法,经过不断完善,现在把费曼积分计算问题彻底转换为了线性代数问题。在该方法中,只要能够求解出一组线性方程组,就可以首先把一般性多圈费曼积分的计算问题简化为相同圈数真空积分的计算问题,然后把待求真空积分计算问题进一步简化为更少圈数的真空积分计算问题,不断循环最后问题归结为已知的单圈真空积分。由于线性代数问题总能够系统地求解(只要有足够的计算资源),因此该方法在国际上首次实现了一般性费曼积分的系统性计算。马滟青课题组已经把该方法用计算机程序实现并开源,基于该程序所有人都能自动化地计算一般性的费曼积分(https://doi.org/10.1016/j.cpc.2022.108565)。目前该方法和程序已被广泛用于粒子物理前沿问题的高精度计算。
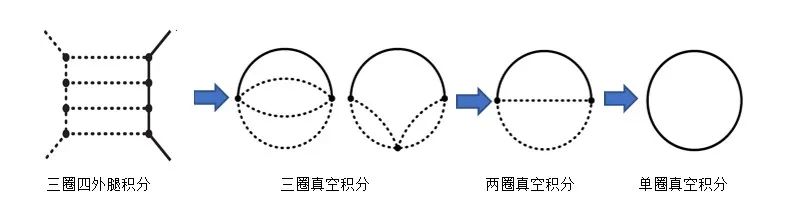
辅助质量流方法的工作流程
该系列工作中,马滟青课题组的研究生刘霄(目前是英国牛津大学博士后)、王辰宇(目前是德国卡尔斯鲁厄大学博士后)和刘志峰(目前博士在读)先后做出了重要贡献。
研究工作得到了国家自然科学基金、科技部重点研发计划和永利集团高性能计算平台的支持。
论文原文链接
https://doi.org/10.1103/PhysRevLett.129.222001
其他相关链接
https://doi.org/10.1016/j.physletb.2018.02.026
https://doi.org/10.1103/PhysRevD.105.L051503
https://doi.org/10.1016/j.cpc.2022.108565


